It goes like velocity squared.

It goes like velocity squared.

Introduction
IN 1720 Willem's Gravesande dropped steel balls into soft clay to discover that the work done in the collision was proportional to the velocity of the ball squared. Up to this point theorists had stressed the importance of momentum which was proportional to velocity. His work was recognized by Emilie du Chatelet and was eventually used to define the important concept of kinetic energy.
Material
Florist foam (the softest possible)(For example we use "Artesia Wet Floral Foam." although we use it dry.)
Steel Ball Bearings (we use 1/2 inch or 1 cm diameter)
meter stick
PVC tube 3/4 inch diameter Schedule 40, in lengths of 0.5 m, 1 m, and 2 m (optional PVC pipe connector)
wooden dowel 1/4 inch diameter at least 4 inches long.

To Do and Notice
Place the PVC pipe on one surface of the foam block.
Drop the ball into the pipe.

Remove the pipe and notice the ball has penetrated the block of foam.

Remove the ball and insert the dowel into the resulting hole. Make a mark on the dowel at the top surface of the foam.

Measure the depth of the hole.
Try this for drops of 0.5 m, 1.0 m, and 2.0 m (See the introductory image above.)
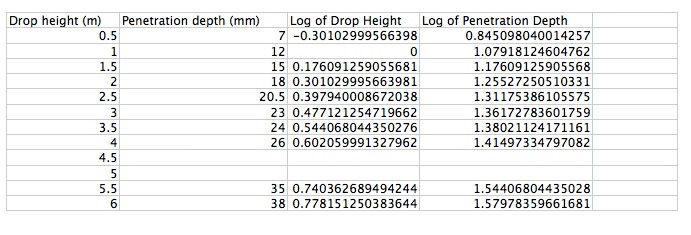
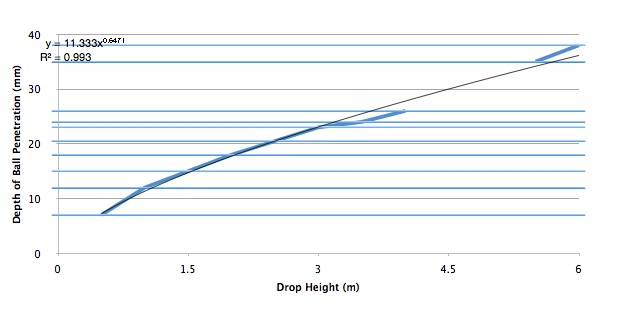
Our steel balls penetrated
| 0.5 m | 0.9 cm |
| 1.0 m | 1.4 cm |
| 2.0 m | 2.0 cm |
What's Going On?
The foam we used required a spring like force to push the ball bearing into the foam.
The force, F, resisting motion increased as the depth, x, of penetration increased, like a spring F = k * x where k is a constant.
The work done as the foam is compressed is them W = F * x (integrated over the path length) giving the work to compress a spring W = 1/2 k x^2
A ball of mass , m, dropped a distance h converts a potential energy of mgh into kinetic energy KE = 1/2 mv^2 , where g is the acceleration of gravity.
This kinetic energy is converted into work penetrating the foam mgh = 1/2 mv^2 = 1/2 k x^2
or x = (2mg/k)^0.5 * h^0.5 so the depth of penetration is proportional to the square root of the initial height.
Also x = (m/k)^0.5 v so depth is proportional to velocity.
The soft clay used by Gravesande exerted a constant force F = C, this means that a similar constant force applied to the ball bearing would cause it to move at a constant speed through the clay. This definitely does not happen with the foam. His clay must have been behaved like a liquid for high velocities and as a solid for low velocities....the opposite of the behavior of cornstarch and water, perhaps we should use ketchup?)
In this case the equations become mgh = 1/2 mv^2 = Cx
So the depth x = (mg/C) x and the depth is proportional to the height.
and depth x = 1/2 m/C v^2 so depth is proportional to velocity squared.
The appearance of the velocity squared in the energy term caused him to hypothesize the existence of "Vis Viva" which we know as kinetic energy.
Etc
Voltaire called Emilie du Chatelet "A great man, whose only fault was being a woman.
http://en.wikipedia.org/wiki/Émilie_du_Châtelet#Advocacy_of_kinetic_energy

|
Scientific Explorations with Paul Doherty |
|
16 November 2011 |