Gray Step

Math Root

When the boundary between two gray gradients is covered you do not see the change in brightness from one side to the other.

By examining the finite difference derivatives of the grayness of the postcard we can get an idea of what the eye and brain do when they analyze an image.

Here is a good image of a gradient in darkness from left to right, repeated twice.

A linear gradient in gray from light to dark repeated twice. Click for an enlarged image.

Define the grayness of a piece of the gray step postcard, G, as the fraction of the incident light that is absorbed by the postcard.

The grayness of the gray step postcards increases linearly from G = 0.1 at the left edge to G = 0.2 at the center. Then it repeats, changing abruptly to G = 0.1 and increasing to G = 0.2 again at the right edge.

Define a coordinate system with x = 0 at the center of the postcard.
The postcard exists for -10 cm < x < 10 cm.

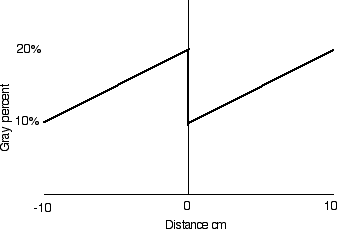
Gray percent versus distance on the postcard.

Write an equation for grayness versus x.
x >0 G = 0.1 + x * (0.1/10)
x< 0 G = 0.2 + x * (0.1/10)

There is a problem at x = 0 where there is a discontinuity.

The cones on the retina have a finite size. This allows us to get around the mathematical difficulty at the origin by creating a table of values of grayness versus position. We can then perform finite difference mathematics on the table.

Let's break the gray step postcard into 1 cm wide regions and write the average grayness in each region:

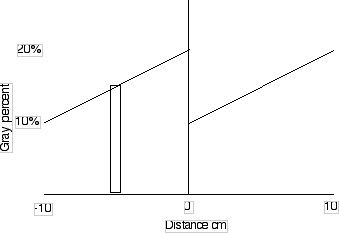
A one centimeter wide region at -5 cm or -0.05 m is 15% gray.

Make a table for every 1 cm wide interval.

x	-.1	-.09	-.08	-.07	-.06	-.05	-.04	-.03	-.02	-.01	0	.01	.02	.03	.04	.05	.06	.07	.08	.09	.1
G	.1	.11	.12	.13	.14	.15	.16	.17	.18	.19	.15	.11	.12	.13	.14	.15	.16	.17	.18	.19	.2

Now let's compute the central finite difference derivative.

dG/dx = (G(x+1) - G(x-1))/((x+1)-(x-1)) = (G(x+1) - G(x-1))/2 m^-1

For Example dG(-.09)/dx = (.12-.1)/2 = .02/2 = .01 m^-1

x	-.1	-.09	-.08	-.07	-.06	-.05	-.04	-.03	-.02	-.01	0	.01	.02	.03	.04	.05	.06	.07	.08	.09	.1
G	---	.01	..01	.01	.01	.01	.01	.01	.01	.01	-.04	.01	.01	.01	.01	.01	.01	.01	.01	.01	---

This table does not contain enough information to allow the retina to determine which side is dark and which side is bright. It shows that there is an edge in the center.

Let's press on and take the second finite difference derivative by applying the same rule over again.

d²G/dx² = d(dG/dx)/dx = (dG(x+1)/dx - dG(x-1)/dx)/((x+1)-(x-1))

x	-.1	-.09	-.08	-.07	-.06	-.05	-.04	-.03	-.02	-.01	0	.01	.02	.03	.04	.05	.06	.07	.08	.09	.1
G	.---	---	.0	0	0	0	0	0	0	-.025	0	.025	0	0	0	0	0	0	0	---	---

Here we can see that to the left of the center the cells are all the same, 0, except for the one cell just left of the center which is -.025. While to the right the cells are also 0 except for the one that is +.025. These positive and negative values of the second derivative give each side of the gray step its dark or light value. The zeros give each side a constant shading.

Return to Gray Step

Scientific Explorations with Paul Doherty

© 1999

22 June 99