tidalevolution

Tidal Evolution of a Planet and its Moon

The Earth and Moon

It is obvious that when viewed from the earth the same side of the moon faces toward the earth at all times, the side with the man in the moon.

What an amazing result. For this to happen the moon must rotate once every orbit.

As a result of this coupling between the moons orbit and its rotation, when viewed from the moon's surface the earth stays in the same place in the sky at all times.

Pluto and Charon

Pluto has a moon Charon. Charon also points one side toward Pluto at all times. So Pluto remains in the same place in the Charon sky at all times. However, Pluto also keeps one side turned toward Charon, so Charon remains in the same place in the skies of Pluto at all times.

Pluto spins on its axis once in 6.39 earth days, Charon spins on its axis once in 6.39 earth days and the period of Charon's orbit is 6.39 earth days. The rotation of Pluto is retrograde. This means that viewed from above the northern hemisphere of the earth Pluto spins clockwise.

Tides

If you live near an ocean then you have experienced tides. There are two high tides a day.

There are also tides in the solid earth. The tidal bulge is about 1 meter high. The moon pulls up this tidal bulge on the earth, there is a time delay between the pull of the moon and the time when the tidal bulge reaches its maximum height. During this time the rotation of the earth carries this tidal bulge around the planet in the direction of rotation.

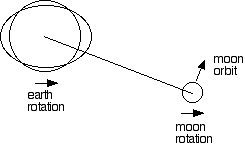
Viewed from above the north pole, the earth and moon rotate and the moon orbits counterclockwise.
The earth rotates faster than the moon orbits so earth tides are pulled ahead of the earth moon line.
Illustration is not to scale, the moon is much farther away.

The moon then pulls on the mass of the tidal bulge and slows the rotation of the earth.

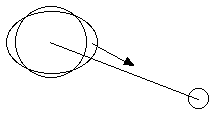
The moon pulls on the tidal bulge of the earth slowing the rotation of the earth.
It pulls on the near bulge more than on the far bulge.

Fossil horn corals put down one growth ring every day in a pattern that is modulated by months and years. They record that 300 million years ago there were 400 days per year. The length of the day at that time was 22 hours. (24 * 365/400 = 22 )

Today, the rotation of the earth is still slowing down, the slowing down can be measured by atomic clocks. A "leap" second has to be added to our clocks almost every year to correct for the slowing of the rotation of the earth.

The earth pulls up a much larger tidal bulge on the moon. If the moon were rotating so that we could see different regions of the moon then the rotation of the moon would carry the tidal bulges forward in the direction of rotation and the earth would pull on these tidal bulges slowing the moon until it rotated once per orbit keeping the same face toward the earth. This is what has happened to our moon and to almost every other moon in the solar system, they all keep one face toward their planet. (Except for Hyperion which orbits Saturn.)

Charon is a massive moon relative to its planet, Charon has slowed the rotation of Pluto until both objects keep one face toward each other.

The tidal bulges on the earth, which have been pulled in front of the earth moon line by the rotation of the earth, also exert forces on the orbit of the moon. The tidal bulges pull the moon forward in its orbit adding energy to the orbit. The moon moves into a higher orbit with time. This causes the month to get longer. Laser retroreflectors left on the moon by the Apollo astronauts have allowed us to measure the distance to the moon with centimeters of accuracy. These measurements show that the radius of the moons orbit is increasing.

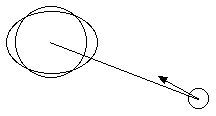
The near tidal bulge on the earth pulls the moon forward in its orbit. Adding energy to the moon's orbit and moving the moon into a larger radius orbit with a longer period.

Mars and Phobos

Phobos is the inner moon of Mars. It orbits every 7.7 earth hours. Mars rotates in 24.66 earth hours. Viewed from above the north pole of the earth, Mars rotates counterclockwise and Phobos orbits counterclockwise. (As do the earth and its moon.)

Yet Phobos orbits so much faster than Mars rotates that Phobos rises in the west and sets in the east.

The tidal bulge pulled up on Mars by Phobos lags behind the planet-moon line. The tidal bulge removes energy from Phobos' orbit. Phobos is spiraling in toward Mars and will be torn apart into a temporary ring sometime in the next few hundred million years, "soon" in the life of the solar system.

Math Root

The height of a tidal bulge on a planet is proportional to the inverse cube of the distance between the planet and the object causing the tidal bulge. The torque which slows down the planet is proportional to the inverse sixth power of the distance.