Introduction

A basket type coffee filter will reach terminal velocity after falling a very short distance. The terminal velocity depends on several things such as the mass of the coffee filter its area and its shape.

Material

• Basket type coffee filters
• 2, meter sticks
• tape
• stopwatches

Assembly

Tape the meter sticks together.

To Do and Notice

Drop the coffee filter and observe it fall. It seems to fall at constant speed.

Use the stopwatch to time how long it takes the filter to fall the first meter and then the second. How much does the speed change?

Nest one coffee filter inside another, this nested pair will have twice the mass and the same cross sectional area as a single one.
Drop the single one side by side with the double.
Notice, the double falls faster.

How much faster?

Find the two heights so that the two filters when released together hit the floor at the same time.
For example, drop the single filter from 1 meter high, then the double from 1.6 meters. The single will hit the floor first. Find the height from which to drop the double so that it its the floor at the same time, perhaps 1.4 m or so.

See the image at the top of the page.

Compare the fall of 4 nested filters with a single filter. Once again drop the single from 1 meter above the floor. Find the height from which the quadruple nest hits the floor at the same time as the single.

Gather data on height for simultaneous arrival versus the number of filters.
(Notice that the time it takes for the single filter to drop a meter is always the same.
The multi-filter stack falls farther in this time, and so the stack falls faster!)

Plot the data as a graph of height of drop for multiple stack versus number of filters in the stack.

What’s Going On?

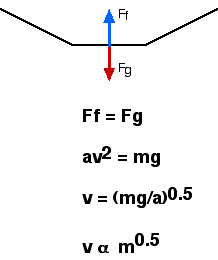
Terminal velocity occurs when the net force on a falling object goes to zero.
No net force means no acceleration.
There are two forces on the object gravity and air resistance.
The gravity force is proportional to the mass.
The air resistance is proportional to the cross sectional area of the filter.
Air resistance also increases as the speed increases, for coffee filters the air resistance force is proportional to the square of the speed of fall.
A heavier filter with the same area as a lighter one must fall faster to reach terminal velocity. So more massive filter stacks have a higher terminal velocity and fall further in the same time.

Math Root

The gravity force is

F_g = mg

where m is the mass of the object and
g is the acceleration of gravity g = 10 m/s².

The air resistance force is

F_a = (1/2) C_d A r v²

where A is the cross sectional area of the filter, the area of its shadow from a light which is straight above it
v is the speed of the fall
r is the density of the air
and C_d is the drag coefficient which is a dimensionless fudge factor describing the effect of the shape.

Aerodynamicists throw in the 1/2 so that this equation is simply related to other equations such as the Bernoulli equation.

At terminal velocity

F_g= F_a

mg = 1/2 C_d A r v²

solving for v

v = (2 m g/C_d A r)^1/2

so the terminal velocity is proportional to the square root of the mass.

Notice the units of A r v^2,, it has the units of force, and so the drag coefficient is dimensionless.

By the way if you plot your terminal velocity versus the number of nested filters, i.e. the mass, on log-log paper the slope of the straight line gives you the proportionality, the slope should be 1/2.

Math Root 2

Calculate the Reynolds Number for the falling filters.

The Reynolds number, R, helps discriminate between laminar and turbulent flow around an object.

R = r v L/h

where r is fluid density for air = 1.2 kg/m^3

v is velocity = 0.85 m/s

L is the dimension of the object = 15 cm diameter = 0.15 m

and h is viscoscity for air = 1.8 * 10^-5  m^2/s

calculating R = 8500 

Definitely turbulent.

Etc

The drag coefficient, C_d, for the coffee filter is just about 1.0

Going Further

Find different size basket type coffee filters and muffin holders. Measure the terminal velocity of these different size objects.

Scientific Explorations with Paul Doherty

© 2000

27 October 2000