 Here's
how it can be done.
Here's
how it can be done.Jump into the air, you can turn your body.
Physicists assure us that an object in the air that is not turning cannot start to turn.
They call this the law of conservation of angular momentum.
However, a person in the air can turn to face a new direction without violating the law of conservation of angular momentum. And, a cat can turn over while falling to always land on its feet.
 Here's
how it can be done.
Here's
how it can be done.![]()
I face you.
I jump into the air, and while I am in the air you point to one side or the other.
I turn in midair and face that direction.
Since I didn't know which way I was going to turn when I left the ground, I could not have cheated by starting my rotation before I left the ground.
If you do not have fast reactions then you can try this acivity off a diving board or on a trampoline.
A Step by step analysis:
Here is a basic way to make a turn while keeping your angular mementum zero.
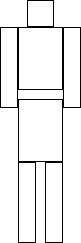
Think of your body as two parts, above the waist and below the waist, above the waist you have arms which you can stick out or pull in.
Below the waist you have legs which can do the same.
Start
Both parts start facing north, 0 degrees. Leap into the air. Your assistant points east.

Twist 1
Legs in, arms out. Rotate about your middle so your legs face a little beyond east, 100 degrees. With your legs together your bottom half rotates easily, with your arms out your upper body is more difficult to rotate. Your upper body rotates a little to the west, to -10 degrees. The angular momenta of your upper and lower body cancel, there is no net angular momentum at any time.
. ..........................
..........................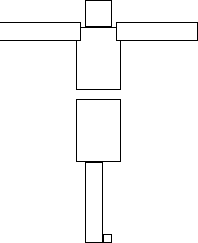
Twist 2
Now stick out your legs, tuck in your arms, and rotate your upper body to face east.
 .................................
.................................![]()
Your upper body easily rotates through 100 degrees, from -10 degrees to 90 degrees.
Your lower body with its legs out is hard to rotate, so it rotates a little the other way, from 100 degrees to 90 degrees.
Bring your legs together and land
Both parts are facing east.
At all times the sum of the angular momentum of the upper and of the lower body have cancelled, that is the sum is zero.
Math Root
The angular momentum, L, is the product of the angular velocity, w, and the moment of inertia, I.
L = wI
(It takes me a half second to turn 90 degrees. My angular velocity is 90 degrees in 1/2 second or 180 degrees per second. However angular velocity, w, must be expressed in radians per second! So convert from degrees to radians to get about 3 radians per second.)
The moment of inertia measures how hard it is to change the rotation of an object. It depends on the mass, m, and the distribution of the mass.
Different objects have different moments of inertia.
The moment of inertia of a thin walled hollow cylinder of radius, r , is
I = mr^2
If the body is made of two halves the upper half with its arms spread out has a large moment of inertia say Iu = 10 kgm^2 and the lower half with legs in has a small moment of inertia, Il = 1. If the upper half has angular velocity wu and the lower half wl and if the total angular momentum the sum of these two and is zero!
0 = wu Iu + wl Il
0 = wu 10 +wl 1
so 10 wu = -wl
or wu = -wl/10
the upper body rotates opposite the lower body but only with 1/10 the angular velocity.
The total angle that one half of the body rotates through is w t where t is the time of the rotation so the upper body rotates 1/10 as far as the lower body.
In the second half of this problem the lower body with legs out has a moment of inertia that is large, say 10 , while the upper half with arms in is small, 1.
The result of one rotation followed by the other is that the body ends up rotating through 90 degrees while at all times its angular momentum is zero.